kmf = KaplanMeierFitter().fit(df['T'], df['E'])
kmf.plot(figsize=(11,6));
To borrow a term from finance, we clearly have different regimes that a customer goes through: periods of low churn and periods of high churn, both of which are predictable. This predictability and "sharp" changes in hazards suggests that a piecewise hazard model may work well: hazard is constant during intervals, but varies over different intervals.
Furthermore, we can imagine that individual customer variables influence their likelihood to churn as well. Since we have baseline information, we can fit a regression model. For simplicity, let's assume that a customer's hazard is constant in each period, however it varies over each customer (heterogeneity in customers). Hat tip to StatWonk for this model:
Our hazard model looks like¹: $$ h(t\;|\;x) = \begin{cases} \lambda_0(x)^{-1}, & t \le \tau_0 \\ \lambda_1(x)^{-1} & \tau_0 < t \le \tau_1 \\ \lambda_2(x)^{-1} & \tau_1 < t \le \tau_2 \\ ... \end{cases} $$
and \(\lambda_i(x) = \exp(\mathbf{\beta}_i x^T), \;\; \mathbf{\beta}_i = (\beta_{i,1}, \beta_{i,2}, ...)\). That is, each period has a hazard rate, \(\lambda_i\), that is the exponential of a linear model. The parameters of each linear model are unique to that period - different periods have different parameters (later we will generalize this).
Why do I want a model like this? Well, it offers lots of flexibility (at the cost of efficiency though), but importantly I can see:
- Influence of variables over time.
- Looking at important variables at specific "drops" (or regime changes). For example, what variables cause the large drop at the start? What variables prevent death at the second billing?
- Predictive power: since we model the hazard more accurately (we hope) than a simpler parametric form, we have better estimates of a subjects survival curve.
One interesting point is that this model is not an accelerated failure time model even though the behaviour in each interval looks like one. This is because the breakpoints (intervals) do not change in response (contract or dilate) to the covariates (but that's an interesting extension).
¹ I specify the reciprocal because that follows lifelines convention for exponential and Weibull hazards. In practice, it means the interpretation of the sign is possibly different.
pew = PiecewiseExponentialRegressionFitter(
breakpoints=breakpoints)\
.fit(df, "T", "E")
Above we fit the regression model. We supplied a list of breakpoints that we inferred from the survival function and from our domain knowledge.
Let's first look at the average hazard in each interval, over time. We should see that during periods of high customer churn, we also have a high hazard. We should also see that the hazard is constant in each interval.
fig, ax = plt.subplots(1,1)
kmf.plot(figsize=(11,6), ax=ax);
ax.legend(loc="upper left")
ax.set_ylabel("Survival")
ax2 = ax.twinx()
pew.predict_cumulative_hazard(
pew._norm_mean.to_frame(name='average hazard').T,
times=np.arange(0, 110),
).diff().plot(ax=ax2, c='k', alpha=0.80)
ax2.legend(loc="upper right")
ax2.set_ylabel("Hazard")
It's obvious that the highest average churn is in the first few days, and then high again in the latter billing periods.
So far, we have only been looking at the aggregated population - that is, we haven't looked at what variables are associated with churning. Let's first start with investigating what is causing (or associated with) the drop at the second billing event (~day 30).
fig, ax = plt.subplots(figsize=(10, 4))
pew.plot(parameter=['lambda_2_'], ax=ax);
From this forest plot, we can see that the var1 has a protective effect, that is, customers with a high var1 are much less likely to churn in the second billing periods. var2 has little effect, but possibly negative. From a business point of view, maximizing var1 for customers would be a good move (assuming it's a causal relationship).
We can look at all the coefficients in one large forest plot, see below. We see a distinct alternating pattern in the _intercepts variable. This makes sense, as our hazard rate shifts between high and low churn regimes. The influence of var1 seems to spike in the 3rd interval (lambda_2_), and then decays back to zero. The influence of var2 looks like it starts to become more negative over time, that is, is associated with more churn over time.
fig, ax = plt.subplots(figsize=(10, 10))
pew.plot(ax=ax);
Regularization as a model parameter
If we suspect there is some parameter sharing between intervals, or we want to regularize (and hence share information) between intervals, we can include a penalizer which penalizes the variance of the estimates per covariate.
Note: we do not penalize the intercept, currently. This is a modelers decision, but I think it's better not too.
Specifically, our penalized log-likelihood, \(PLL\), looks like:
$$ PLL = LL - \alpha \sum_j \hat{\sigma}_j^2 $$where \(\hat{\sigma}_j\) is the standard deviation of \(\beta_{i, j}\) over all periods \(i\). This acts as a regularizer and much like a multilevel component in Bayesian statistics. In the above inference, we implicitly set \(\alpha\) equal to 0. Below we examine some more cases of varying \(\alpha\). First we set \(\alpha\) to an extremely large value, which should push the variances of the estimates to zero.
# Extreme case, note that all the covariates' parameters are almost identical.
pew = PiecewiseExponentialRegressionFitter(
breakpoints=breakpoints,
penalizer=20.0)\
.fit(df, "T", "E")
fig, ax = plt.subplots(figsize=(10, 10))
pew.plot(ax=ax);
As we suspected, a very high penalizer will constrain the same parameter between intervals to be equal (and hence 0 variance). This is the same as the model:
$$ h(t\;|\;x) = \begin{cases} \lambda_0(x)^{-1}, & t \le \tau_0 \\ \lambda_1(x)^{-1} & \tau_0 < t \le \tau_1 \\ \lambda_2(x)^{-1} & \tau_1 < t \le \tau_2 \\ ... \end{cases} $$and \(\lambda_i(x) = \exp(\mathbf{\beta_{0,i} + \beta} x^T), \;\; \mathbf{\beta} = (\beta_{1}, \beta_{2}, ...)\). Note the reuse of the \(\beta\)s between intervals.
This model is the same model proposed in "Piecewise Exponential Models for Survival Data with Covariates".
One nice property of this model is that because of the extreme information sharing between intervals, we have maximum information for inferences, and hence small standard errors per parameter. However, if the parameters effect is truly time-varying (and not constant), then the standard error will be inflated and a less constrained model is better.
Below we examine a in-between penalty, and compare it to the zero penalty.
# less extreme case
pew = PiecewiseExponentialRegressionFitter(
breakpoints=breakpoints,
penalizer=.25)\
.fit(df, "T", "E")
fig, ax = plt.subplots(figsize=(10, 10))
pew.plot(ax=ax, fmt="s", label="small penalty on variance")
# compare this to the no penalizer case
pew_no_penalty = PiecewiseExponentialRegressionFitter(
breakpoints=breakpoints,
penalizer=0)\
.fit(df, "T", "E")
pew_no_penalty.plot(ax=ax, c="r", fmt="o", label="no penalty on variance")
plt.legend();
We can see that:
- on average, the standard errors are smaller in the penalty case
- parameters are pushed closer together (they will converge to their average if we keep increasing the penalty)
- the intercepts are barely effected.
I think, in practice, adding a small penalty is the right thing to do. It's extremely unlikely that intervals are independent, and extremely unlikely that parameters are constant over intervals.
Like all lifelines models, we have prediction methods too. This is where we can see customer heterogeneity vividly.
# Some prediction methods
pew.predict_survival_function(df.loc[0:3]).plot(figsize=(10, 5));
pew.predict_cumulative_hazard(df.loc[0:3]).plot(figsize=(10, 5));
pew.predict_median(df.loc[0:5])
Conclusion
In conclusion, this model is pretty flexible and it is one that can encourage more questions to be asked. Beyond just SaaS churn, one can think of other application of piecewise regression models: employee churn after their stock option vesting cliff, mortality during different life stages, or modelling time-varying parameters.
Future extensions include adding support for time-varying covariates. Stay tuned!
We can see that the fit is pretty good, but there is some non-linearities in the second figure we aren't capturing. We should expect non-linearities too: in the batch algorithm, the average batch size is (N * frac) data points, so this interaction should be a factor in the batch algorithm's performance. Let's include that interaction in our regression:
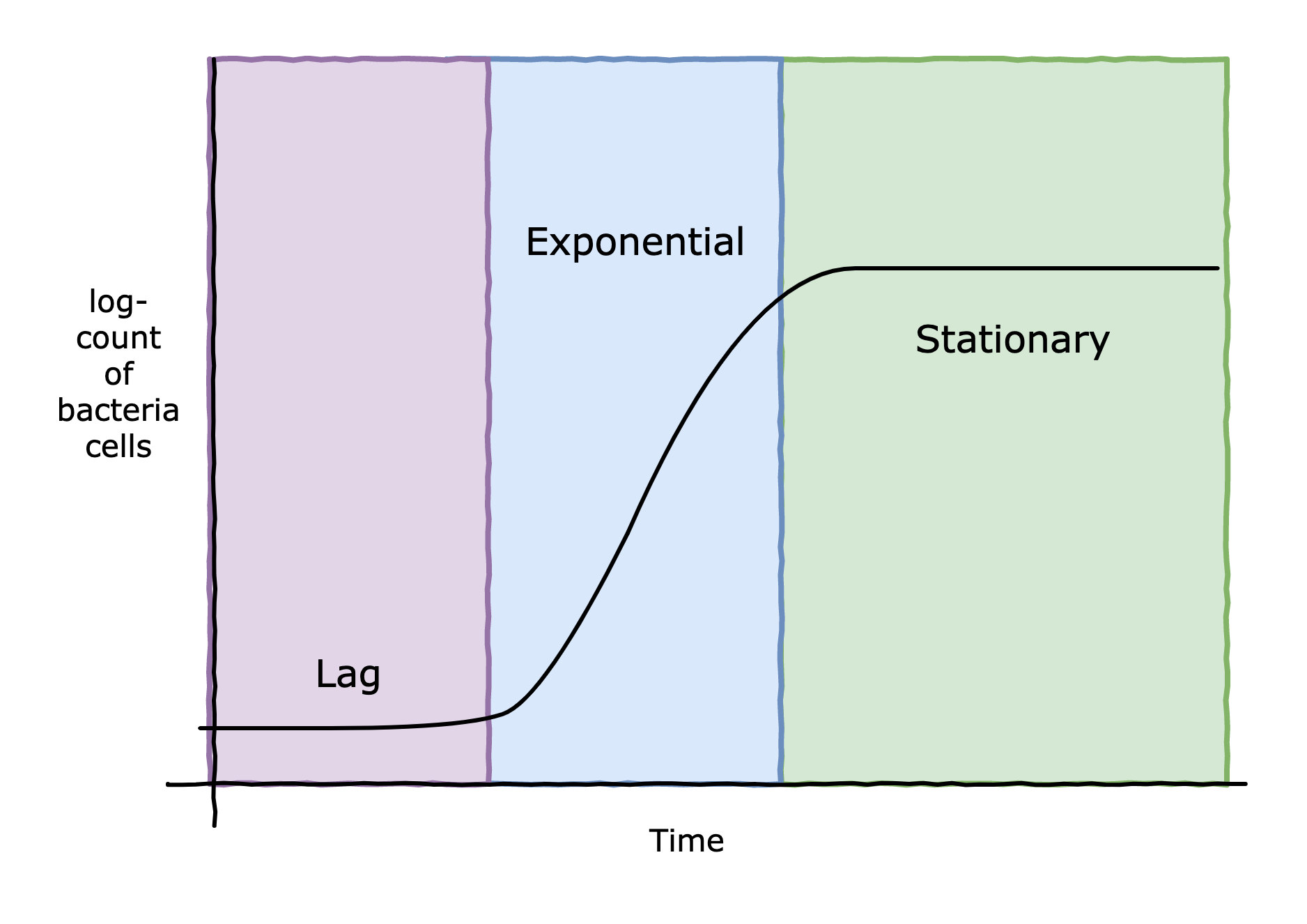
However, hurdle technology is at play here. The idea is to use multiple hurdles, in this case salt, acid, and enough competing microbes, to effectively pause any botulism bacteria in their lag period. The salt is added in the brine, and the acid can be provided by the lactic acid bacteria or manually added to the brine. For brines below 6% NaCl, which almost all fermentation brines are, the lactic acid bacteria have essentially no lag period and very quickly enter their exponential phase [1]. However, C. Botulinum can survive moderate amounts of salt as well, and if present, could also start multiplying. What we'd like is to create an environment that extends the lag period of C. Botulinum far enough such that the lactic acid bacteria can completely out compete any C. Botulinum present. Let's get some data.
